How To Find One To One Function Inverse
Inverse Functions: One to I
Not all functions take inverse functions. The graph of inverse functions are reflections over the line y = x. This means that each x-value must exist matched to one and merely i y-value. Functions that run across this criteria are called ane-to one functions.
DEFINITION OF I-TO-One:
A function is said to be one-to-one if each 10-value corresponds to exactly one y-value.
A role f has an inverse function, f -1, if and just if f is i-to-one.
A quick test for a one-to-i function is the horizontal line examination. If a horizontal line intersects the graph of the part in more than one identify, the functions is NOT 1-to-one.
HORIZONTAL LINE Examination:
A part f is one-to-one and has an changed function if and only if no horizontal line intersects the graph of f at more one point.
Let's apply this feature to determine if a role has an inverse.
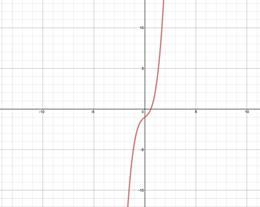
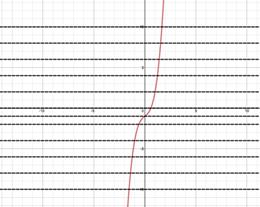
Example one: Use the Horizontal Line Exam to decide if f(x) = 2xiii - 1 has an inverse function.
| Step 1: Sketch the graph of the function. | |
| Step ii: Apply the Horizontal Line Examination. Visualize multiple horizontal lines and look for places where the graph is intersected more than once. No horizontal line intersects the graph in more than than i place and thus the function has an inverse. | |
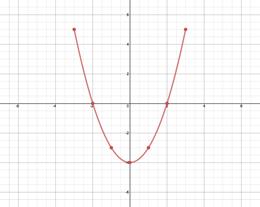
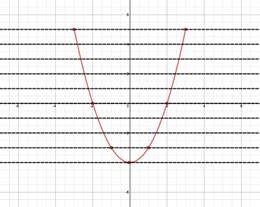
Example two: Sketch the graph represented by the points and determine if information technology has an inverse office.
| x | -3 | -2 | -i | 0 | 1 | 2 | 3 |
| y | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
| Step 1: Sketch the graph of the role. | | ||||||||||||||||
| Step ii: Utilise the Horizontal Line Test. Visualize multiple horizontal lines and look for places where the graph is intersected more than than once. Several horizontal lines intersect the graph in two places. Thus the function is not a one-to-i and does non have an inverse. Also detect that if the ordered pairs are switched, this results in repeating x-values and a role cannot have repeating x-values.
| |
Source: https://www.softschools.com/math/pre_calculus/inverse_functions_one_to_one/
Posted by: hendrixdesten.blogspot.com


0 Response to "How To Find One To One Function Inverse"
Post a Comment